Johannes Kepler (1610), autor desconhecido
Conhecido(a) por
Leis de Kepler
Nascimento
27 de dezembro de 1571
Weil der Stadt
Morte
15 de novembro de 1630 (58 anos)
Ratisbona, Baviera, Alemanha
Alma mater
Universidade de Tübingen
Assinatura
Unterschrift Kepler.svg
Orientador(es)
Michael Maestlin[1]
Instituições
Universidade de Linz
Campo(s)
Astronomia, astrologia, matemática, filosofia natural
Johannes Kepler (Weil der Stadt, 27 de dezembro de 1571 — Ratisbona, 15 de novembro de 1630) foi um astrônomo, astrólogo [2] e matemático alemão. Considerado figura-chave da revolução científica do século XVII, é todavia célebre por ter formulado as três leis fundamentais da mecânica celeste, denominadas por Leis de Kepler, tendo estas sido codificadas por astrônomos posteriores com base nas suas obras Astronomia Nova, Harmonices Mundi, e Epítome da Astronomia de Copérnico. Essas obras também forneceram uma das bases para a teoria da gravitação universal de Isaac Newton.
Durante sua carreira, Kepler foi professor de matemática em uma escola seminarista em Graz, Áustria, um assistente do astrônomo Tycho Brahe, o matemático imperial do imperador Rodolfo II e de seus dois sucessores, Matias I e Fernando II. Também foi professor de matemática em Linz, Áustria, e conselheiro do general Wallenstein. Adicionalmente, fez um trabalho fundamental no campo da ótica, inventou uma versão melhorada do telescópio refrator (o telescópio de Kepler) e ajudou a legitimar as descobertas telescópicas de seu contemporâneo Galileu Galilei.
Kepler viveu numa época em que não havia nenhuma distinção clara entre astronomia e astrologia, mas havia uma forte divisão entre a astronomia (um ramo da matemática dentro das artes liberais) e a física (um ramo da filosofia natural). Kepler também incorporou raciocínios e argumentos religiosos em seu trabalho, motivado pela convicção religiosa de que Deus havia criado o mundo de acordo com um plano inteligível, acessível através da luz natural da razão.[3] Kepler descreveu sua nova astronomia como "física celeste",[4] como "uma excursão à Metafísica de Aristóteles"[5] e como "um suplemento de Sobre o Céu de Aristóteles",[6] transformando a antiga tradição da cosmologia física ao tratar a astronomia como parte de uma física matemática universal.[7]
Índice
- 1Primeiros anos
- 2Graz (1594–1600)
- 3Praga (1600–1612)
- 4Outros trabalhos em matemática e física
- 5Problemas pessoais e políticos
- 6Linz e outros lugares (1612–1630)
- 7Recepção à sua astronomia
- 8Legado cultural e histórico
- 9Obras
- 10Ver também
- 11Notas e referências
- 12Bibliografia
Primeiros anos
O Grande Cometa de 1577, que Kepler viu quando criança, e que atraiu a atenção de astrônomos na Europa.
Local de nascimento de Johannes Kepler, em Weil der Stadt
Johannes Kepler nasceu em 27 de dezembro de 1571, na cidade imperial livre Weil der Stadt (agora parte da Região de Estugarda no estado alemão Baden-Württemberg, 30 km a oeste do centro de Estugarda). Seu avô, Sebald Kepler, tinha sido lorde-prefeito daquela cidade, mas, quando Johannes nasceu, tinha dois irmãos e uma irmã e a fortuna da família Kepler estava em declínio. Seu pai, Heinrich Kepler, ganhava a vida de maneira precária como um mercenário, e deixou a família quando Johannes tinha cinco anos de idade. Acreditava-se que tinha morrido na Guerra dos Oitenta Anos nos Países Baixos. Sua mãe, Katharina Guldenmann, a filha de um dono de hospedaria, era uma curandeira e herbolária que mais tarde foi julgada por bruxaria. Nascido prematuramente, Johannes disse ter sido uma criança fraca e doente. Ele foi, no entanto, uma criança brilhante; e frequentemente impressionava viajantes na pousada de seu avô com sua fenomenal capacidade matemática.[8]
Kepler foi apresentado à astronomia quando criança, e desenvolveu um amor por ela que manteve por toda sua vida. Aos seis anos de idade, observou o Grande Cometa de 1577, deixou escrito que "foi levado por sua mãe para um local elevado para vê-lo."[9] Aos nove anos, observou um outro evento astronômico, um eclipse lunar em 1580, registrando que se lembrava de ter sido "chamado para fora" para observá-lo e que a lua "parecia bastante vermelha".[9] No entanto, varíola durante a infância o deixou com a visão fraca e alguma invalidez nas mãos, limitando sua habilidade para os aspectos observacionais da astronomia.[10]
Em 1589, depois de ter passado pela escola primária, escola de latim, e seminário em Maulbronn, Kepler começou a assistir as aulas de Tübinger Stift na Universidade de Tubinga. Lá, estudou filosofia, tendo Vitus Müller como professor[11] e teologia tendo Jacob Heerbrand como professor (um estudante de Philipp Melanchthon em Wittenberg), que também ensinou Michael Maestlin quando esse era um estudante.[12] Kepler provou ser um matemático excepcional e ganhou uma reputação de astrólogo hábil, fazendo horóscopos para colegas estudantes. Sob a instrução de Michael Maestlin, professor de matemática de Tübingen de 1583 até 1631,[12] ele aprendeu tanto o sistema ptolomaico quanto o sistema copernicano dos movimentos planetários. Ele se tornou um copernicano na época. Em um debate estudantil, defendeu o heliocentrismo de uma perspectiva tanto teórica quanto teológica, mantendo que o Sol era a principal fonte de poder motriz no Universo.[13] Apesar de seu desejo de se tornar um ministro, perto do fim de seus estudos Kepler foi recomendado para uma posição de professor de matemática e astronomia na escola protestante de Graz (mais tarde a Universidade de Graz). Ele aceitou a posição em abril de 1594, quando tinha 23 anos de idade.[14]
Graz (1594–1600)
Mysterium Cosmographicum
O modelo de Kepler dos sólidos platônicos para o Sistema Solar, do Mysterium Cosmographicum (1600)
O primeiro grande trabalho sobre astronomia de Johannes Kepler, Mysterium Cosmographicum (O Mistério Cosmográfico), foi a primeira defesa publicada do sistema copernicano. Kepler afirmou ter tido uma epifania em 19 de julho de 1595, enquanto ensinava em Graz, enquanto explicava a conjunção periódica de Saturno e Júpiter no zodíaco; ele percebeu que polígonos regulares limitavam um círculo inscrito e um círculo circunscrito em razões definidas, que, ele raciocinou, poderiam ser a base geométrica do universo. Após não conseguir encontrar um arranjo único de polígonos que se ajustasse às observações astronômicas conhecidas (mesmo com planetas extras adicionados ao sistema), Kepler começou a experimentar com poliedros, figuras tri-dimensionais. Ele descobriu que cada um dos cinco sólidos platônicos podia ser inscrito e circunscrito de forma única por esferas celestes; aninhando-se estes sólidos, cada um envolto por uma esfera, cada um dentro do outro, produzia-se seis camadas, correspondentes aos seis planetas conhecidos — Mercúrio, Vênus, Terra, Marte, Júpiter, e Saturno. Ao ordenar os sólidos corretamente —octaedro, icosaedro, dodecaedro, tetraedro, cubo— Kepler descobriu que as esferas podiam ser posicionadas em intervalos correspondentes (dentro dos limites de acurácia das observações astronômicas disponíveis) ao tamanho relativo de cada trajetória planetária, assumindo-se que os planetas giram em torno do Sol. Kepler também encontrou uma fórmula que relacionava o tamanho da esfera de cada planeta com a duração de seu período orbital: dos planetas interiores aos exteriores, a razão de aumento do período orbital é o dobro da diferença entre os raios das esferas. No entanto, mais tarde Kepler rejeitou esta fórmula, porque ela não era precisa o suficiente.[15]
Como ele indicou no título, Kepler pensou que havia revelado o plano geométrico de Deus para o Universo. Muito do entusiasmo de Kepler pelo sistema copernicano vinha de suas convicções teológicas a respeito da conexão entre o físico e o espiritual; o próprio Universo era uma imagem de Deus, com o Sol correspondendo ao Pai, e a esfera estelar ao Filho, e o espaço intermediário entre eles ao Espírito Santo. Seu primeiro manuscrito de Mysterium continha um extenso capítulo reconciliando o heliocentrismo com passagens bíblicas que pareciam sustentar o geocentrismo.[16]
Com o apoio de seu mentor Michael Maestlin, Kepler recebeu permissão do senado da Universidade de Tübingen para publicar seu manuscrito, pendendo remoção da exegese bíblica e a adição de uma descrição mais simples e entendível do sistema copernicano assim como das novas ideias de Kepler. Mysterium foi publicado nos finais de 1596, e Kepler recebeu suas cópias e começou a enviá-las a proeminentes astrônomos e patronos dos começos de 1597; não foi amplamente lido, mas estabeleceu a reputação de Kepler como astrônomo muito habilidoso. A efusiva dedicação a patronos poderosos, assim como aos homens que controlavam sua posição em Graz, também forneceu uma porta de entrada decisiva para o sistema de patronagem.[17]
Seção interna do modelo.
Apesar dos detalhes terem sido modificados à luz de seus trabalhos posteriores, Kepler nunca renunciou à cosmologia platonista poliédrica-esferista apresentada em Mysterium Cosmographicum. Suas principais obras de astronomia subsequentes foram de certa forma, apenas desenvolvimentos adicionais dela, preocupados em encontrar dimensões interiores e exteriores mais precisas para as esferas, por meio do cálculo das excentricidades das órbitas planetárias dentro delas. Em 1621, Kepler publicou a segunda edição de Mysterium, expandida, uma metade a mais que a primeira, detalhando em notas de rodapé as correções e melhorias que ele tinha alcançado após 25 anos desde sua primeira publicação.[18]
Em termos de impacto, Mysterium pode ser visto como um importante primeiro passo na modernização da teoria copernicana. Não há dúvidas de que objetivo de "De Revolutionibus" de Copérnico foi o de promover um sistema heliocêntrico, mas nesse livro ele recorreu a artifícios ptolemaicos (epiciclos e círculos excêntricos) a fim de explicar a mudança na velocidade orbital dos planetas. Além disso, Copérnico continuou a usar como ponto de referência o centro da órbita terrestre em vez da do Sol, como dito por ele, "como um auxílio para as contas e a fim de não confundir o leitor por divergir muito de Ptolomeu." Portanto, embora a tese do "Mysterium Cosmographicum" estivesse errada, a astronomia moderna deve muito a esse trabalho "uma vez que representa o primeiro passo na limpeza do sistema copernicano dos remanescentes da teoria ptolomaica ainda agarrados a ela." [19]
Casamento com Barbara Müller
Retratos de Kepler e sua esposa.
Em dezembro 1595, Kepler foi apresentado a Barbara Müller, de 23 anos de idade, viúva (duas vezes) e com uma filha pequena, Gemma van Dvijneveldt, e ele começou a cortejá-la. Müller, herdeira dos bens de seus maridos falecidos, também era a filha de um bem-sucedido dono de um moinho. Seu pai, Jobst, inicialmente se opôs ao casamento, apesar da nobreza de Kepler; embora ele tivesse herdado a nobreza de seu avô, sua pobreza fazia dele um partido inaceitável. Jobst cedeu após Kepler completar sua obra Mysterium, mas o acordo quase se desfez enquanto Kepler estava longe cuidando dos detalhes para a publicação. No entanto, oficiais da igreja —que tinham ajudado a estabelecer o casamento— pressionaram os Müllers a honrar com seu acordo. Barbara e Johannes se casaram em 27 de abril de 1597.[20]
Nos primeiros anos do seu casamento, os Keplers tiveram dois filhos (Heinrich e Susanna), que morreram na infância. Em 1602, eles tiveram uma filha (Susanna); em 1604, um filho (Friedrich); e em 1607, outro filho (Ludwig).[21]
Outras pesquisas
Após a publicação de Mysterium e com a bênção dos inspetores escolares de Graz, Kepler começou um ambicioso programa para estender e elaborar suas obras. Ele planejou quatro livros adicionais: um sobre os aspectos estacionários do Universo (o Sol e as estrelas fixas); um sobre os planetas e seus movimentos; um sobre a natureza física dos planetas e a formação das características geográficas (focado especialmente na Terra); e um sobre os efeitos dos céus sobre a Terra, incluindo óptica atmosférica, meteorologia e astrologia.[22]
Ele também procurou as opiniões de muitos dos astrônomos aos quais tinha enviado Mysterium, entre eles Reimarus Ursus (Nicolaus Reimers Bär) —o matemático imperial de Rodofo II e um rival mordaz de Tycho Brahe. Ursus não respondeu diretamente, mas republicou a carta lisonjeira de Kepler, a fim de vencer sua disputa contra Tycho, a respeito da primazia do (como é agora chamado) sistema tychonico. Apesar disso, Tycho também começou a trocar correspondências com Kepler, começando com uma crítica severa, mas legítima, do sistema de Kepler; dentre uma série de objeções, Tycho declarou ser um problema o uso de dados numéricos imprecisos de Copérnico. Através de suas cartas, Tycho e Kepler discutiram sobre uma ampla gama de problemas de astronomia, entre eles, fenômenos lunares e a teoria copernicana (particularmente, a sua viabilidade teológica). Mas sem os dados significativamente mais precisos do observatório de Tycho, Kepler não tinha como tratar de muitas dessas questões.[23]
Em vez disso, ele voltou sua atenção para a cronologia e "harmonia", as relações numerológicas entre a música, matemática e o mundo físico, e suas consequências astrológicas. Assumindo que a Terra possuía uma alma (uma propriedade que mais tarde ele invocaria para explicar como o Sol causa o movimento dos planetas), ele estabeleceu um sistema especulativo que conectava aspectos astrológicos e distâncias astronômicas ao clima e outros fenômenos terrestres. Por volta de 1599, entretanto, novamente ele sentiu seu trabalho limitado pela imprecisão dos dados disponíveis —assim como uma crescente tensão religiosa que também estava ameaçando a continuação de seu emprego em Graz. Em dezembro daquele ano, Tycho convidou Kepler a visitá-lo em Praga; em 1º de janeiro de 1600 (antes mesmo de ele receber o convite), Kepler partiu na esperança de que a patronagem de Tycho poderia resolver seus problemas filosóficos assim como os sociais e financeiros.[24]
Praga (1600–1612)
Trabalho para Tycho Brahe
Em 4 de fevereiro de 1600, Kepler encontrou Tycho Brahe e seus assistentes Franz Tengnagel e Longomontanus em Benátky nad Jizerou (a 35 km de Praga), o local onde o novo observatório de Tycho estava sendo construído. Nos dois meses seguintes, ele permaneceu como um convidado, analisando algumas das observações de Tycho a respeito de Marte; Tycho vigiava de perto os seus dados, mas ficou impressionado com as ideias teóricas de Kepler e logo lhe permitiu mais acesso. Kepler planejava testar sua teoria[25]exposta no Mysterium Cosmographicum baseando-se nos dados sobre Marte, mas ele estimou que o trabalho levaria até dois anos (uma vez que ele não tinha permissão para simplesmente copiar os dados para seu próprio uso). Com a ajuda de Johannes Jessenius, Kepler tentou negociar um arranjo de emprego mais formal com Tycho, mas as negociações acabaram em uma discussão furiosa, e Kepler partiu para Praga em 6 de abril. Kepler e Tycho logo se reconciliaram e finalmente chegaram a um acordo sobre o salário e condições de moradia, e em junho, Kepler retornou a sua casa em Graz para reunir-se com sua família.[26]
Dificuldades politicas e religiosas em Graz arrancaram suas esperanças de retornar imediatamente a Tycho; na esperança de continuar seus estudos de astronomia, Kepler procurou uma nomeação como matemático do arquiduque Fernando. Com esse objetivo, Kepler compôs um ensaio — dedicado a Fernando — em que propunha uma teoria baseada em forças para o movimento da Lua: "In Terra inest virtus, quae Lunam ciet" ("Há uma força na Terra que faz com que a lua se mova").[27] Embora o ensaio não tenha lhe rendido um lugar na corte Fernando, ele continha detalhes a respeito de um novo método para mensurar eclipses lunares, que ele aplicou durante o eclipse de 10 de julho em Graz. Essas observações formaram a base de suas explorações das leis da óptica que culminariam em seu Astronomiae Pars Optica.[28]
Em 2 de agosto de 1600, após se recusar a converter-se ao catolicismo, Kepler e sua família foram banidos de Graz. Meses depois, Kepler retornou a Praga, agora com o restante de sua família. Durante a maior parte de 1601, Kepler foi diretamente financiado por Tycho, que o designou para analisar observações planetárias e escrever um trato contra o rival de Tycho (então falecido), Ursus. Em setembro, Tycho garantiu-lhe uma comissão para que fosse colaborador no novo projeto que ele tinha proposto ao imperador: as tábuas rudolfinas que deveriam substituir as tábuas prutênicas de Erasmus Reinhold. Dois dias após a morte inesperada de Tycho em 24 de outubro de 1601, Kepler foi nomeado seu sucessor como matemático imperial com a responsabilidade de completar seu trabalho inacabado. Os próximos onze anos como matemático imperial foram os mais produtivos de sua vida.[29]
Conselheiro do imperador Rodolfo II
A obrigação primária de Kepler como matemático imperial era dar conselhos astrológicos para o imperador. Embora Kepler tivesse uma visão negativa das tentativas de astrólogos contemporâneos de predizer precisamente o futuro ou eventos divinos específicos, ele projetava bem-recebidos detalhados horóscopos para amigos, família e patronos desde seu tempo como estudante em Tübingen. Além de horóscopos para aliados e líderes estrangeiros, o imperador buscava os conselhos de Kepler em tempos de problemas políticos (no entanto, as recomendações de Kepler eram baseadas mais em bom senso do que nas estrelas). Rodolfo se interessava ativamente pelo trabalho de vários dos estudiosos de sua corte (incluindo numerosos alquimistas) e manteve-se a par do trabalho de Kepler em astronomia física.[30]
Oficialmente, as únicas doutrinas religiosas aceitáveis em Praga eram a Católica e a Utraquista, mas a posição de Kepler na corte imperial permitiu-lhe praticar sua fé luterana desimpedido. O imperador nominalmente abastecia a família de Kepler com um ampla renda, mas das dificuldades do crédito sobrecarregado do tesouro imperial decorria que realmente obter dinheiro suficiente para cumprir com as obrigações financeiras era uma luta ininterrupta. Parcialmente por causa de problemas financeiros, sua vida domiciliar com Barbara era desagradável, marcada por brigas e crises de doença. A vida na corte, no entanto, levou Kepler a ter contanto com outros proeminentes estudiosos (Johannes Matthäus Wackher von Wackhenfels, Jost Bürgi, David Fabricius, Martin Bachazek, e Johannes Brengger, entre outros) e seu trabalho astronômico avançou rapidamente.[31]
Astronomiae Pars Optica
Uma página do Astronomiae Pars Optica, ilustrando a estrutura de olhos
Ao passo que ele lentamente continuava a analisar as observações de Tycho a respeito de Marte —agora à sua disposição em sua totalidade— e começava o lento processo de tabulação das tábuas rudolfinas, Kepler também retomou a investigação a respeito das leis da óptica de seu ensaio de 1600 sobre a Lua. Tanto o eclipse lunar quanto o solar apresentavam fenômenos não explicados, tais como tamanhos inesperados para as sombras, a cor vermelha de um eclipse lunar total, e a luz incomum ao redor de um eclipse solar total que tinha sido por alguns noticiada. Questões relacionadas de refração atmosférica se aplicavam a todas as observações astronômicas. Durante a maior parte do ano de 1603, Kepler fez uma pausa em seu outro trabalho para focar na teoria óptica; o manuscrito resultante, apresentado ao imperador em 1º de janeiro de 1604, foi publicado com o título Astronomiae Pars Optica (A Parte Óptica da Astronomia). Nessa obra, Kepler descreveu a lei do inverso do quadrado da distância que governa a intensidade da luz, reflexão por espelhos planos e curvos, e princípios das câmeras estenopeicas, assim como as implicações da óptica para a astronomia, tais como a paralaxe e os tamanhos aparentes dos corpos celestes. Ele também estendeu seu estudo de óptica ao olho humano, e é geralmente considerado por neurocientistas como o primeiro a perceber que as imagens são projetadas invertidas e são revertidas pelo cristalino na retina. A solução para esse dilema não era de particular importância para Kepler porque ele não o via como dizendo respeito à óptica, embora ele tenha sugerido que a imagem era mais tarde corrigida "nas cavidades do cérebro" devido à "atividade da alma".[32] Atualmente, Astronomiae Pars Optica é geralmente reconhecido como a fundação da óptica moderna (embora a lei da refração não apareça nele).[33]
Kepler e a física do corpo humano
Johannes Kepler é muitas vezes lembrado em função da descoberta das leis dos movimentos planetários (lei da forma elíptica, lei das áreas e lei harmônica) mas também teve suma importância em outros campos do conhecimento humano, no que diz respeito à física do corpo humano. Um desses campos é a óptica. Kepler foi um dos precursores da "óptica geométrica", visto que seus estudos embasaram o conhecimento desta área e o conceito de óptica geométrica foi fruto de um intenso enfoque de Kepler na aplicação das leis de refração da luz. A óptica do início do século XVII já contava com progressos importantes relacionados a seção estudada por Kepler, podem ser citadas contribuições de alguns cientistas: Felix Plater, no campo anatômico. Este descobriu que o principal componente do olho, no ato da visão, é a retina, responsável pela formação das imagens dos objetos vistos, rompendo, assim, com a tradição galênica, representada principalmente por Alhazen, Bacon e Vitélio, para a qual é no cristalino que se forma a imagem; Alhazen, no campo matemático : seus trabalhos, mais tarde continuados por Bacon, Pecham e Vitélio admitiram a abordagem geométrico-óptica do cone visual de Euclides e Ptolomeu, na qual o ápice do cone está no olho e a sua base no objeto visto, desenvolvendo-a até chegar à concepção de que há uma correspondência ponto a ponto entre imagem e objeto; no campo técnico, a interessante analogia entre a câmara escura, um artefato mecânico, com o olho humano, um órgão natural, feita por Alhazen, Leonardo da Vinci e Porta, na qual o olho humano é análogo à câmara escura, que projeta a imagem invertida do objeto em sua tela, o que ocorre também no olho humano. Tendo por base, os conhecimentos citados, até ao início do século 17 foi decidido que uma imagem é formada no olho sobre a superfície anterior da lente cristalina. Todavia, entrou em cena Johanes Kepler, que sem executar novas experiências, e unicamente pela aplicação das leis de refração da luz, analisou o caminho da luz através do olho e demonstrou que uma imagem é formada sobre a retina, e também que esta é invertida. A aceitação desta descoberta foi impedida por preconceitos contemporâneos, visto que os cientistas da época apenas conseguiam compreender uma imagem direita no olho. Com a descoberta do caminho da luz no olho de Kepler, foi possível explicar os seguintes fenômenos físicos: acuidade visual central, campo visual, adaptação ao escuro, e erros de refração. Diplopia fisiológica e mecanismo de acomodação, tiveram sua explicação um pouco mais tarde. A lei afirmando que a intensidade da luz diminui com o quadrado da distância também foi formulada por Johannes Kepler. Esta lei, também, só poderia ser demonstrada após o caminho da luz através do olho tinha sido descoberto. Nos últimos anos, o telescópio Kepler assumiu um significado prático em óptica oftalmológica. Como um auxiliar de leitura para as pessoas com deficiência visual que oferece uma ampliação significativamente maior do que qualquer outro recurso visual óptica, mostrando a importância de Kepler na área da óptica contemporânea.[34][35]
A Supernova de 1604
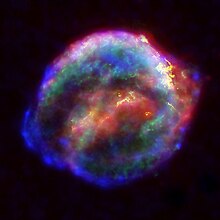
Remanescente da Supernova de Kepler (SN 1604).
Em outubro de 1604, uma nova estrela bastante brilhante (SN 1604) apareceu, mas Kepler não acreditou nos rumores até que ele mesmo a viu. Kepler começou a observar sistematicamente a estrela. Astrologicamente, o final de 1603 marcava o começo de um trígono de fogo, o começo do ciclo de grandes conjunções de ca. 800 anos; astrólogos associaram os dois prévios períodos desse tipo com a ascensão de Carlos Magno (ca. 800 anos antes) e o nascimento de Cristo (cerca de 1600 anos antes), e assim esperavam eventos grandiosos, especialmente em relação ao imperador. Foi nesse contexto, como matemático imperial e astrólogo do imperador, que Kepler descreveu a nova estrela dois anos depois em seu De Stella Nova. Nele, Kepler tratou a respeito das propriedades astronômicas da estrela, tendo uma atitude cética para as muitas interpretações astrológicas então em circulação. Ele percebeu sua luminosidade em enfraquecimento, especulou a respeito de sua origem, e usou a falta de paralaxe observada para argumentar que ela estava na esfera de estrelas fixas, minando ainda mais a doutrina da imutabilidade dos céus (a ideia aceita desde Aristóteles de que as esferas celestiais eram perfeitas e imutáveis). O nascimento de uma nova estrela implicava a variabilidade dos céus. Em um apêndice, Kepler também discutiu o então recente trabalho cronológico do historiador polonês Laurentius Suslyga; ele calculou que, se Suslyga estava correto de que as cronologias aceitas estavam quatro anos atrasadas, então a Estrela de Belém —de maneira análoga à então nova estrela— teria coincidido com a primeira grande conjunção do ciclo de 800 anos anterior.[36]
A localização da stella nova, no pé de Ofiúco, está marcada com um N (localizada 8 quadrículas para baixo e 4 da esquerda para a direita).
Astronomia nova
A ampla linha de investigação que culminou no Astronomia nova (Uma Nova Astronomia) —incluindo as primeiras duas leis do movimento planetário— começou com a análise, sob a direção de Tycho, da órbita de Marte. Kepler calculou e recalculou várias aproximações da órbita de Marte usando um equante (a ferramenta matemática que Copérnico tinha eliminado com o seu sistema), e por fim criou um modelo que em geral concordava com as observações de Tycho para dentro de dois minutos de arco (o erro médio das medições). Mas ele não ficou satisfeito com o demasiado complexo e ainda levemente pouco preciso resultado; em certos pontos o modelo diferia dos dados por até oito minutos de arco. Nenhum dos vários métodos de astronomia matemática tradicionais logrou o fim em vista, e foi então que Kepler começou a tentar encaixar uma órbita oval para os dados.[37]
Na visão religiosa de Kepler do cosmos, o Sol (um símbolo de Deus, o Pai) era a fonte da força motiva no sistema solar. Para embasamento físico, Kepler usou de analogia com a teoria de William Gilbert da alma magnética da Terra encontrada em De Magnete (1600) e em suas próprias pesquisas em óptica. Kepler supôs que o poder motivo (ou espécies motivas)[38] irradiado pelo Sol enfraquecia com a distância, causando movimento mais rápido ou lento a medida que os planetas se moviam para mais próximo ou longe dele.[39][40] Talvez esta suposição implicasse uma relação matemática que restaurasse a ordem astronômica. Baseado em medições do afélio e periélio da Terra e Marte, ele criou uma fórmula em que a taxa de movimento de um planeta é inversamente proporcional a sua distância ao Sol. Verificar essa relação para todo o ciclo orbital, no entanto, requeria cálculos muito extensos; assim, para simplificar essa tarefa, até o final de 1602 Kepler reformulou a proporção em termos geométricos: os planetas varrem áreas iguais em tempos iguais —A segunda lei de Kepler do movimento planetário.[41]
Diagrama da trajetória geocêntrica de Marte através de vários períodos de aparente movimento retrógrado. Astronomia nova, Capítulo 1, (1609).
Ele então começou a calcular toda a órbita de Marte, usando a lei da taxa geométrica e assumindo uma órbita em formato de ovo (ovoide). Após aproximadamente 40 tentativas fracassadas, no começo de 1605 ele finalmente teve a ideia de usar uma elipse, que ele tinha anteriormente assumido que era uma solução simples demais para que astrônomos anteriores a tivessem negligenciado. Após constatar que uma órbita elíptica se ajustava aos dados de Marte, ele imediatamente concluiu que todos os planetas movem-se em elipses, com o Sol em um dos focos —A primeira lei de Kepler do movimento planetário. Por não empregar assistentes de cálculo, no entanto, ele não estendeu sua análise matemática para além de Marte. Pelo final do ano, ele completou o manuscrito de Astronomia nova, contudo, ele não seria publicado até 1609 devido a disputas legais sobre o uso das observações de Tycho, de propriedade de seus herdeiros.[42]
Dioptrice, o manuscrito Somnium e outro trabalho
![]() Ver artigo principal: Somnium
Ver artigo principal: Somnium
Nos anos seguintes à conclusão do Astronomia Nova, a maior parte das pesquisas de Kepler estava focada em preparações para as tábuas rudolfinas e um conjunto abrangente de efemérides (previsões específicas acerca das posições de planetas e estrelas) baseadas na tabela (embora ainda por muitos anos nenhum desses trabalhos seria concluído). Ele também tentou (sem sucesso) começar uma colaboração com o astrônomo italiano Giovanni Antonio Magini. Alguns de seus outros trabalhos tratavam de cronologia, especialmente a datação de eventos da vida de Jesus, e com astrologia, especialmente críticas a previsões dramáticas de catástrofes, como as de Helisaeus Roeslin.[43]
Kepler e Roeslin travaram uma série de ataques e contra-ataques públicos, enquanto o físico Philip Feselius publicou uma obra que descartava completamente a astrologia (e o trabalho de Roeslin em particular). Em resposta ao que Kepler viu por um lado como excessos da astrologia e por outro como rejeição excessiva a ela, Kepler preparou Tertius Interveniens (As intervenções de terceiros). Esse trabalho —apresentado ao patrono em comum de Roeslin e Feselius— era uma mediação neutra entre estudiosos rivais, mas também apresentava as visões gerais de Kepler sobre o valor da astrologia, incluindo alguns mecanismos conjecturados de interação entre planetas e almas individuais. Enquanto Kepler considerava a maioria das regras e métodos tradicionais da astrologia como sendo "esterco fedorento" em que "uma galinha diligente" arranha, havia "talvez, também um pouco de grão bom" para ser encontrado pelo astrólogo científico consciente.[44]
A rua Karlova na Cidade Antiga, Praga – casa em que Johannes Kepler viveu. [1] Museu
Nos primeiros meses de 1610, Galileu Galilei —usando seu poderoso novo telescópio— descobriu quatro satélites orbitando Júpiter. Galileu escreveu Sidereus Nuncius (O Mensageiro das Estrelas) descrevendo suas descobertas, e solicitou o parecer de Kepler (em parte para reforçar a credibilidade de suas observações). Kepler respondeu com entusiasmo, com uma resposta curta publicada com o título Dissertatio cum Nuncio Sidereo (Diálogo com o Mensageiro das Estrelas). Kepler endossou as observações de Galileu e ofereceu várias especulações a respeito dos significados e implicações dessas descobertas, além de métodos telescópicos, para astronomia e óptica assim como para cosmologia e astrologia. Mais tarde no mesmo ano, Kepler publicou suas próprias observações telescópicas das luas em Narratio de Jovis Satellitibus, proporcionando ainda mais apoio a Galileu. No entanto, para o desapontamento de Kepler, Galileu nunca publicou suas reações (se as houve) ao Astronomia Nova.[45]
Após ficar sabendo das descobertas telescópicas de Galileu, Kepler também começou uma investigação teórica e experimental da óptica dos telescópios usando um telescópio emprestado por Duque Ernesto de Colônia.[46] O manuscrito resultante foi concluído em setembro de 1610 e publicado como Dioptrice em 1611. Nele, Kepler estabeleceu as bases teóricas a respeito das lentes convergentes duplamente convexas e lentes convergentes duplamente côncavas —e como elas podem ser combinadas para produzir um telescópio galileano— assim como os conceitos de imagens reais e virtuais, direitas e invertidas, e os efeitos da distância focal sobre a magnificação e redução. Ele também descreveu um telescópio aprimorado —agora conhecido como telescópio astronômico ou telescópio kepleriano— em que duas lentes convexas são capazes de produzir maior ampliação do que uma combinação de lentes convexas e côncavas como no de Galileu.[47]
Um dos diagramas de Strena Seu de Nive Sexangula, ilustrando a conjectura de Kepler
Por volta de 1611, Kepler fez circular um manuscrito do que viria a ser publicado (postumamente) como Somnium (O Sonho). Parte do objetivo do Somnium era descrever como seria a prática de astronomia da perspectiva de outra planeta, para mostrar a viabilidade de um sistema não geocêntrico. O manuscrito, que desapareceu depois de mudar de proprietário várias vezes, descrevia uma fantástica viagem à lua; e parte alegoria, parte autobiografia, e parte um tratado sobre viagens interplanetárias (e às vezes é descrita como a primeira obra de ficção científica). Anos depois, uma versão distorcida da história pode ter instigado o julgamento por bruxaria contra sua mãe, uma vez que a mãe do narrador consulta um demônio para aprender os meios de realizar viagens espaciais. Após a sua eventual absolvição, Kepler compôs 223 notas de rodapé para a história —que juntas eram várias vezes mais extensas do que o próprio texto— que explicavam os aspectos alegóricos, bem como o considerável conteúdo científico (particularmente a respeito da geografia lunar) escondidos dentro do texto.[48]
Outros trabalhos em matemática e física
Como presente de ano novo, ele também compôs para o seu amigo e há algum tempo patrono, Baron Wackher von Wackhenfels, um pequeno folheto intitulado Strena Seu de Nive Sexangula (Um Presente de Ano Novo de Neve Hexagonal). Neste tratado, Kepler publicou a primeira descrição da simetria hexagonal dos flocos de neve e, estendeu a discussão para uma hipotética base física atomística para a simetria e enunciou o que mais tarde ficou conhecida como a conjectura de Kepler, uma afirmação a respeito da disposição mais eficiente para o empacotamento de esferas.[49][50] Kepler foi um dos pioneiros em relação às aplicações matemáticas dos infinitesimais (veja-se lei da continuidade).
Problemas pessoais e políticos
Em 1611, a crescente tensão política-religiosa em Praga chegou a um cume. O imperador Rodolfo II —cuja saúde estava em declínio— foi forçado a abdicar ao posto de rei da Boêmia por seu irmão Matias. Ambos os lados procuraram os conselhos astrológicos de Kepler, uma oportunidade que ele aproveitou para fornecer aconselhamento político visando conciliação (com pouca referência às estrelas, exceto em declarações gerais para desencorajar ações drásticas). No entanto, ficou claro que as perspectivas futuras de Kepler na corte de Matias não eram boas.[51]
Também no mesmo ano, Barbara Kepler contraiu febre maculosa húngara, e começou a ter convulsões. Enquanto Barbara se recuperava, todos os três filhos de Kepler sentiram-se doentes e descobriu-se que tinham contraído varíola; Friedrich, com 6 anos, morreu. Após a morte de seu filho, Kepler enviou cartas a patronos em potencial em Württemberg e Pádua. Na Universidade de Tübingen em Württemberg, preocupações a respeito do que percebiam como heresias calvinistas de Kepler em violação à Confissão de Augsburgo e à Fórmula da Concórdia impediram seu retorno. A Universidade de Pádua —sob recomendação de Galileu que estava a deixando— buscou Kepler para preencher a cátedra de matemática, mas Kepler, preferindo manter sua família em território alemão, preferiu viajar à Áustria para conseguir uma posição de professor distrital de matemática em Linz. Contudo, Barbara teve uma recaída na doença e morreu pouco depois do retorno de Kepler.[52]
Kepler postergou a mudança para Linz e permaneceu em Praga até a morte de Rodolfo nos inícios de 1612, embora entre agitação política, tensão religiosa, e tragédia familiar (juntamente com a disputa legal sobre os bens de sua esposa), Kepler estava impossibilitado de fazer qualquer pesquisa. Em vez disso, ele uniu num todo um manuscrito sobre cronologia, Eclogae Chronicae, de correspondências e trabalhos anteriores. Após a sucessão como Imperador do Sacro Império Romano, Matias reafirmou a posição (e salário) de Kepler como matemático imperial, mas permitiu-lhe mudar-se para Linz.[53]
Linz e outros lugares (1612–1630)
Uma estátua de Kepler em Linz.
Em Linz, as principais responsabilidades de Kepler (além de completar as tábuas rudolfinas) eram lecionar na escola distrital e prestar serviços astrológicos e astronômicos. Em seus primeiros anos lá, ele desfrutou de segurança financeira e liberdade religiosa se comparada à sua vida Praga —embora tenha sido excluído da Eucaristia por sua igreja luterana devido a suas ideias sobre teologia. Sua primeira publicação em Linz foi De vero Anno (1613), um tratado sobre o ano do nascimento de Cristo; ele também participou de deliberações a respeito da introdução do calendário gregoriano às terras protestantes da Alemanha; naquele ano ele também escreveu o influente tratado matemático Nova stereometria doliorum vinariorum, sobre a mensuração do volume de recipientes com formas tais quais às de barris de vinho, e que foi publicado em 1615.[54]
Segundo casamento
Em 30 de outubro de 1613, Kepler casou-se com Susanna Reuttinger de 24 anos de idade. Após a morte de sua primeira esposa, Barbara, Kepler tinha analisado 11 diferentes noivas em potencial. Ele eventualmente escolheu a Reuttinger, que, Kepler escreveu, "conquistou-me com seu amor, lealdade, poucos gastos domésticos, diligência, e o amor que proveu a seus enteados."[55] As três primeiras crianças deste casamento (Margareta Regina, Katharina, e Sebald) morreram na infância. Outras três atingiram a idade adulta: Cordula (n. 1621); Fridmar (n. 1623); e Hildebert (n. 1625). De acordo com os biógrafos de Kepler, esse foi um casamento muito mais feliz do que o primeiro.[56]
Epítome da Astronomia Copernicana, calendários e o julgamento de sua mãe por bruxaria
Desde a conclusão de Astronomia nova, Kepler tinha a intenção de compor um livro-texto de astronomia.[57] Em 1615, ele completou o primeiro de três volumes de Epitome astronomiae Copernicanae (Epítome da Astronomia de Copérnico); o primeiro volume (livros I–III) foi impresso em 1617, o segundo (livro IV) em 1620, e o terceiro (livros V-VII) em 1621. Apesar do título, que referia-se apenas a heliocentrismo, o livro de Kepler culminou em descrever seu próprio sistema baseado em elipses. O Epitome tornou-se o mais influente livro de Kepler. Ele continha todas as três leis do movimento planetário e buscava explicar os movimentos celestes através de causas físicas.[58] Embora explicitamente estendesse as duas primeiras leis do movimento planetário (aplicadas à Marte em Astronomia nova) para todos os planetas assim como a Lua e os satélites mediceanos de Júpiter, ele não explicava como órbitas elípticas podiam ser obtidas a partir dos dados observados.[59]
Além das tábuas rudolfinas e as, intimamente conectadas a ela, Efemérides, Kepler publicou calendários astrológicos, que foram muito populares e ajudaram a pagar os custos de produzir seu outro trabalho —especialmente quando o amparo que recebia do tesouro imperial foi encerrado. Em seus calendários —seis dentre 1617 e 1624— Kepler fez previsões acerva das posições dos planetas e do clima, bem como de eventos políticos; estes últimos eram frequentemente de grande precisão, graças à sua aguda percepção das tensões políticas e teológicas de sua época. Por 1624, no entanto, a intensificação dessas tensões e a ambiguidade das profecias acarretaram problemas políticos para Kepler; seu calendário final foi queimado publicamente em Graz.[60]
Harmonias geométricas nos sólidos perfeitos, de Harmonices Mundi (1619)
Em 1615, Ursula Reingold, uma mulher em uma disputa financeira com o irmão de Kepler, Christoph, afirmou que a mãe de Kepler, Katharina, a fizera doente com uma poção maléfica. A disputa se intensificou, e em 1617, Katharina foi acusada de bruxaria; julgamentos por bruxaria eram relativamente comuns na Europa Central naquela época. Começando em agosto de 1620 ela foi encarcerada por 14 meses. Ela foi lançada em outubro de 1621, em parte graças à extensa defesa legal elaborada por Kepler. Os acusadores não tinha nenhuma evidência mais forte do que rumores, juntamente com uma versão distorcida, de segunda mão do Somnium de Kepler, em que uma mulher mistura poções e pede a ajuda de um demônio. Durante o julgamento, Kepler adiou seus outros trabalhos para se concentrar unicamente em sua "teoria harmônica". O resultado, publicado em 1619, foi o Harmonices Mundi ("Harmonia do Mundo").[61]
Harmonices Mundi
![]() Ver artigo principal: Harmonices Mundi
Ver artigo principal: Harmonices Mundi
Kepler tinha convicção de que "os entes geométricos forneceram ao Criador o modelo para decorar o mundo inteiro."[62] Em Harmonia, ele tentou explicar as proporções do mundo natural —particularmente, os aspectos astronômicos e astrológicos— em termos de música. O conjunto central de "harmonias" era a musica universalis ou "música das esferas", que tinha sido estudada por Pitágoras, Ptolomeu e muitos outros antes de Kepler; de fato, logo após a publicação de Harmonices Mundi, Kepler se envolveu em uma disputa de prioridade com Robert Fludd, que tinha recentemente publicado sua própria teoria harmônica.[63]
Kepler começou pela exploração de polígonos regulares e poliedros regulares, incluindo as figuras que seriam mais tarde conhecidas como sólidos de Kepler. A partir daí, ele estendeu sua análise harmônica à musica, meteorologia e astrologia; a harmonia resultava dos tons produzidos pelas almas dos corpos celestes —e, no caso da astrologia, a interação entre esses tons e almas humanas. Na parte final da obra (Livro V), Kepler abordou os movimentos planetários, especialmente as relações entre velocidade orbital e distância orbital ao Sol. Relações semelhantes tinham sido usadas por outros astrônomos, mas Kepler —com os dados de Tycho e suas próprias teorias astronômicas— tratou-as muito mais precisamente e lhes deu novo significado físico.[64]
Dentre muitas outras harmonias, Kepler enunciou o que veio a ser conhecido como a terceira lei do movimento planetário. Em seguida, ele tentou várias combinações até que descobriu que (aproximadamente) "Os quadrados dos períodos estão uns para os outros como os cubos das distâncias médias." Embora ele tenha informado a data dessa epifania (8 de março de 1618), ele não deu detalhes a respeito de como ele chegou a essa conclusão.[65] No entanto, o significado mais profundo para a dinâmica planetária desta lei puramente cinemática não foi percebida até a década de 1660. Uma vez que, quando combinada com a então recente descoberta de Christiaan Huygens da lei da força centrífuga, ela possibilitou a Isaac Newton, Edmund Halley e talvez Christopher Wren e Robert Hooke a perceberem independentemente que a presumida atração gravitacional entre o Sol e seus planetas, se existisse, deveria diminuir com o quadrado da distância entre eles.[66] Isso refutou a hipótese tradicional da física escolástica de que o poder de atração gravitacional se mantinha constante com a distância sempre que aplicado entre dois corpos, tal como assumido por Kepler e também por Galileu em sua equivocada lei universal de que a queda gravitacional é uniformemente acelerada, e também por Borrelli (um estudante de Galileu) em sua mecânica celestial de 1666.[67]William Gilbert, depois de experimentar com ímãs descobriu que o centro da Terra era um enorme ímã. Isso levou Kepler a pensar que uma força magnética do Sol mantinha os planetas em suas órbitas. Era uma explicação interessante para os movimentos dos planetas, mas estava errada. Antes de os cientistas serem capazes de encontrar a resposta correta, eles precisavam saber mais a respeito dos movimentos.
As tábuas rudolfinas e os último anos
O horóscopo feito por Kepler para o General Wallenstein
Em 1623, Kepler finalmente terminou as tábuas rudolfinas, que na época era considerada seu principal trabalho. No entanto, devido aos requerimentos para publicação do imperador e negociações com os herdeiros de Tycho Brahe, não seriam impressas até 1627. Neste meio tempo, tensão religiosa —a causa da então em curso Guerra dos Trinta Anos— mais uma vez colocou Kepler e sua família em perigo. Em 1625, agentes da contra-reforma católica selaram a maior parte da biblioteca de Kepler, e em 1626 a cidade de Linz foi sitiada. Kepler mudou-se para Ulm, onde ele fez arranjos para a impressão das Tábuas às suas próprias despesas.[68]
Em 1628, seguindo-se aos sucessos militares dos exércitos de imperador Fernando sob o comando de General Wallenstein, Kepler tornou-se conselheiro oficial de Wallenstein. Embora não fosse o astrólogo da corte do general propriamente, Kepler fornecia cálculos astronômicos para os astrólogos de Wallenstein e, ocasionalmente, ele mesmo escreveu horóscopos. Em seus últimos anos, Kepler passou grande parte de seu tempo viajando, da corte imperial em Praga até Linz e Ulm para uma moradia temporária em Sagan, e finalmente para Regensburg. Pouco depois de chegar em Regensburg, Kepler adoeceu. Ele morreu em 15 de novembro de 1630, e foi enterrado lá; o local do enterro foi perdido depois que o exército sueco destruiu a igreja.[69] Apenas o epitáfio poético de autoria do próprio Kepler sobreviveu ao tempo:
- Mensus eram coelos, nunc terrae metior umbras
- Mens coelestis erat, corporis umbra iacet.
- Eu medi os céus, agora eu meço as sombras
- Minha mente ao céu esteve presa, o corpo descansa na terra.[70]
Recepção à sua astronomia
As leis de Kepler não foram imediatamente aceitas. Diversas grandes figuras, tais como Galileu e René Descartes ignoraram completamente o Astronomia nova de Kepler. Muitos astrônomos, incluindo o professor de Kepler, Michael Maestlin, fizeram objeções a Kepler pela sua introdução da física em sua astronomia. Alguns outros aceitaram-na parcialmente. Ismael Boulliau aceitou órbitas elípticas mas substituiu a lei de Kepler das áreas por movimento uniforme em relação ao foco vazio da elipse, enquanto Seth Ward usou uma órbita elíptica com movimentos definidos por um equante.[71][72][73]
Muitos astrônomos testaram a teoria de Kepler, e suas diversas modificações, em comparação a observações astronômicas. Dois trânsitos de Vênus e Mercúrio sobre a face do Sol forneceram testes da teoria, sob circunstâncias em que esses planetas não podiam normalmente ser observados. No caso do trânsito de Mercúrio, em 1631, Kepler estava extremamente incerto acerca dos parâmetros para Mercúrio, e aconselhou observadores a esperarem pelo trânsito também nos dias anterior e posterior à data prevista. Pierre Gassendi observou o trânsito na data prevista, uma confirmação da predição de Kepler.[74] Essa foi a primeira observação de um trânsito de Mercúrio. No entanto, sua tentativa de observar o trânsito de Vênus apenas um mês mais tarde, foi mal sucedida devido à inacurácias nas tábuas rudolfinas. Gassendi não ficou sabendo que ele não seria visível a maior parte da Europa, incluindo Paris.[75] Jeremiah Horrocks, que observou o trânsito de Vênus de 1639, tinha usado suas próprias observações para ajustar os parâmetros do modelo de Kepler, previu o trânsito, e depois construiu um aparelho para observá-lo. Ele permaneceu um firme defensor do modelo de Kepler.[76][77][78]
O Epitomo da Astronomia Copernicana foi lido por astrônomos de várias partes da Europa, e após a morte de Kepler foi o principal veículo para a difusão de suas ideias. Entre 1630 e 1650, foi o livro mais utilizado como livro de ensino de astronomia, convertendo muitos para uma astronomia baseada em órbitas elípticas.[58] No entanto, poucos adotaram suas ideias a respeito da base física para movimentos celestiais. Nos finais do século XVII, várias teorias astronômicas físicas inspiradas pelo trabalho de Kepler —notavelmente as de Giovanni Alfonso Borelli e Robert Hooke— começaram a incorporar forças atrativas (embora não as quase-espirituais espécies motivas postuladas por Kepler) e o conceito cartesiano de inércia. Isso culminou no Principia Mathematica (1687) de Isaac Newton, em que Newton derivou as leis de Kepler do movimento planetário de uma teoria baseada na força universal da gravidade.[79]
Legado cultural e histórico
Selo da República Democrática Alemã em homenagem a Kepler.
Além do seu papel no desenvolvimento histórico da astronomia e filosofia natural, Kepler foi importante para a filosofia e historiografia da ciência. Suas leis de movimentos foram centrais para algumas das primeiras histórias da astronomia tais como Histoire des mathématiques (1758) de Jean-Étienne Montucla e Histoire de l’astronomie moderne (1821) de Jean-Baptiste Delambre. Estas e outras histórias escritas de uma perspectiva iluminista trataram os argumentos religiosos e metafísicos de Kepler com ceticismo e desaprovação, mas depois filósofos naturais românticos perceberam estes elementos como centrais ao seu sucesso. William Whewell no seu livro History of the Inductive Sciences (1837), notou Kepler como o arquétipo do gênio científico indutivo; em Philosophy of the Inductive Sciences (1840), Whewell considerou Kepler como a personificação das mais avançadas formas de método científico. Similarmente, Ernst Friedrich Apelt - o primeiro a estudar extensivamente os manuscritos de Kepler após a compra por Catarina, a Grande - identificou Kepler como a chave para a "revolução científica". Apelt que viu a matemática de Kepler, sensibilidade estética, ideias físicas e teologia como parte de um sistema unificado de pensamento, produziu a primeira análise extensiva da vida e trabalho de Kepler.[80]
Traduções modernas de vários livros de Kepler apareceram no final do século XIX e início do século XX, a publicação sistemática de sua coleção de trabalhos começou em 1937 (e está próximo de terminar no início do século XXI), e a biografia feita por Max Caspar foi publicada em 1948.[81] Entretanto, o trabalho de Alexandre Koyré sobre Kepler foi, depois de Apelt, o primeiro marco maior nas interpretações históricas da cosmologia de Kepler e sua influência. Nas décadas de 1930 e 1940 Koyré e outros da primeira geração de historiadores da ciência profissionais, descreveram a "Revolução científica" como o evento central da história da ciência, e Kepler como um (talvez o) personagem central nesta revolução. Koyré colocou a teorização de Kepler, ao invés do seu trabalho empírico, no centro da transformação intelectual das visões antigas para as modernas. Desde a década de 1960, o volume da sabedoria histórica de Kepler se expandiu consideravelmente, incluindo estudos de sua astrologia e meteorologia, seus métodos geométricos, o papel de suas visões religiosas em seus trabalhos, seus métodos de literatura e retórica, sua interação com a cultura geral e correntes filosóficas de seu tempo, e até seu papel como um historiador da ciência.[82]
Monumento a Tycho Brahe e Johannes Kepler em Praga, República Tcheca
O debate sobre o lugar de Kepler na revolução científica produziu também uma grande variedade de tratamentos populares e filosóficos. Um dos mais influentes é The Sleepwalkers (1959) de Arthur Koestler, no qual Kepler é indiscutivelmente o herói (moralmente e teologicamente assim como intelectualmente) da revolução.[83] Filósofos influentes da ciência tais como Charles Sanders Peirce, Norwood Russell Hanson, Stephen Toulmin, e Karl Popper repetidamente voltaram-se a Kepler: exemplos de incomensurabilidade, raciocínio análogo, falseabilidade e muitos outros conceitos filosóficos têm sido encontrados nos trabalhos de Kepler. O físico Wolfgang Pauli até usou a disputa prioritária de Kepler com Robert Fludd para explorar as implicações da psicologia analítica em investigações científicas.[84] Um bem recebido, se irreal, romance histórico de John Banville, Kepler (1981), explorou muitos dos temas desenvolvidos na narrativa não científica de Koestler e na filosofia da ciência.[85] De algum modo mais fantástico é o trabalho de não ficção, Heavenly Intrigue (2004), que sugere que Kepler assassinou Tycho Brahe para ter acesso aos seus dados.[86] Kepler adquiriu uma imagem popular como um ícone da modernidade científica e um homem à frente de seu tempo; Carl Sagan descreveu-o como "o primeiro astrofísico e o último astrólogo científico."[87]
Na Áustria, Kepler deixou um legado histórico tal que foi um dos temas das moedas de pratas de colecionadores, que foi cunhada em 10 de setembro de 2002. O lado reverso da moeda tem um retrato de Kepler, que passou algum tempo ensinando em Graz e áreas em torno. Kepler estava familiarizado pessoalmente com o Príncipe Hans Ulrich von Eggenberg, e provavelmente influenciou a construção do Castelo de Eggenberg (o tema do verso da moeda). Na frente dele na moeda está o modelo de esferas alinhadas e poliedros do Mysterium Cosmographicum.[88]
Em 2009, a NASA nomeou uma sonda espacial, a Kepler, pelas contribuições dele no campo da astronomia.[89]
Obras
- Mysterium cosmographicum (1596)
- De Fundamentis Astrologiae Certioribus (1601)
- Astronomiae Pars Optica (1604)
- De Stella nova in pede Serpentarii (1604)
- Astronomia nova (1609)
- Tertius Interveniens (1610)
- Dissertatio cum Nuncio Sidereo (1610)
- Dioptrice (1611)
- De nive sexangula (1611)
- De vero Anno, quo aeternus Dei Filius humanam naturam in Utero benedictae Virginis Mariae assumpsit (1613)
- Eclogae Chronicae (1615, publicada com Dissertatio cum Nuncio Sidereo)
- Nova stereometria doliorum vinariorum (1615)
- Epitome astronomiae Copernicanae (publicada em três partes dentre os anos 1618 e 1621)
Epitome astronomiae copernicanae, 1618
- Harmonice Mundi (1619)
- Mysterium cosmographicum 2ª edição (1621)
- Tabulae Rudolphinae (1627)
- Somnium (1634)
Ver também
- Heliocentrismo
- História da astronomia
- História da física
- Poliedros de Kepler-Poinsot
- Leis de Kepler
- Revolução copernicana
- Revolução Científica
Notas e referências
- Ir para cima↑ Johannes Kepler (em inglês) no Mathematics Genealogy Project
- Ir para cima↑ Campion, Nicholas (2009). History of western astrology. Volume II, The medieval and modern worlds. primeira ed. [S.l.]: Continuum. ISBN 978-1-4411-8129-9
- Ir para cima↑ Barker and Goldstein, "Theological Foundations of Kepler's Astronomy", pp. 112–13.
- Ir para cima↑ Kepler, New Astronomy, título da página, tr. Donohue, pp. 26–7
- Ir para cima↑ Kepler, New Astronomy, p. 48
- Ir para cima↑ Epitome of Copernican Astronomy in Great Books of the Western World, Vol 16, p. 845
- Ir para cima↑ Stephenson, Kepler's Physical Astronomy, pp. 1–2; Dear, Revolutionizing the Sciences, pp. 74–78
- Ir para cima↑ Caspar. Kepler, pp. 29–36; Connor. Kepler's Witch, pp. 23–46.
- ↑ Ir para:a b Koestler. The Sleepwalkers, p. 234 (translated from Kepler's family horoscope).
- Ir para cima↑ Caspar. Kepler, pp. 36–38; Connor. Kepler's Witch, pp. 25–27.
- Ir para cima↑ Connor, James A. Kepler's Witch (2004), p. 58.
- ↑ Ir para:a b Barker, Peter; Goldstein, Bernard R. "Theological Foundations of Kepler's Astronomy", Osiris, 2nd Series, Vol. 16, Science in Theistic Contexts: Cognitive Dimensions (2001), p. 96.
- Ir para cima↑ Westman, Robert S. "Kepler's Early Physico-Astrological Problematic," Journal for the History of Astronomy, 32 (2001): 227–36.
- Ir para cima↑ Caspar. Kepler, pp. 38–52; Connor. Kepler's Witch, pp. 49–69.
- Ir para cima↑ Caspar. Kepler, pp. 60–65; ver também: Barker and Goldstein, "Theological Foundations of Kepler's Astronomy."
- Ir para cima↑ Barker and Goldstein. "Theological Foundations of Kepler's Astronomy," pp. 99–103, 112–113.
- Ir para cima↑ Caspar. Kepler, pp. 65–71.
- Ir para cima↑ Field. Kepler's Geometrical Cosmology, Chapter IV, p 73ff.
- Ir para cima↑ Dreyer, J.L.E. A History of Astronomy from Thales to Kepler, Dover Publications, 1953, pp. 331, 377-379.
- Ir para cima↑ Caspar, Kepler. pp. 71–75.
- Ir para cima↑ Connor. Kepler's Witch, pp. 89–100, 114–116; Caspar. Kepler, pp. 75–77
- Ir para cima↑ Caspar. Kepler, pp. 85–86.
- Ir para cima↑ Caspar, Kepler, pp. 86–89
- Ir para cima↑ Caspar, Kepler, pp. 89–100
- Ir para cima↑ Using Tycho's data, see 'Two views of a system'
- Ir para cima↑ Caspar, Kepler, pp. 100–08.
- Ir para cima↑ Caspar, Kepler, p. 110.
- Ir para cima↑ Caspar, Kepler, pp. 108–11.
- Ir para cima↑ Caspar, Kepler, pp. 111–22.
- Ir para cima↑ Caspar, Kepler, pp. 149–153
- Ir para cima↑ Caspar, Kepler, pp. 146–148, 159–177
- Ir para cima↑ Finger, "Origins of Neuroscience," p 74. Oxford University Press, 2001.
- Ir para cima↑ Caspar, Kepler, pp. 142–146
- Ir para cima↑ Claudemir Roque Tossato (Oct./Dec. 2007). «Os fundamentos da óptica geométrica de Johannes Kepler». Scielo. Consultado em 7 de agosto de 2016Verifique data em:
|data=(ajuda) - Ir para cima↑ Klin Monbl Augenheilkd (1986 Feb). «Johannes Kepler's contributions to ophthalmologic optics». NCBI. Consultado em 7 de agosto de 2016 Verifique data em:
|data=(ajuda)(em inglês) - Ir para cima↑ Caspar, Kepler, pp. 153–157
- Ir para cima↑ Caspar, Kepler, pp. 123–128
- Ir para cima↑ Sobre espécies motivas, ver: Lindberg, "The Genesis of Kepler's Theory of Light," pp. 38–40
- Ir para cima↑ "A decisão de Kepler de basear sua explicação para a causa dos movimentos planetários em uma lei distância-velocidade, em vez de movimentos circulares uniformes de esferas compostas, marcou uma grande alteração das antigas para as modernas concepções científicas.... [Kepler] tinha começado com princípios físicos e tinha então derivado a trajetória a partir deles, em vez de simplesmente construir novos modelos. Em outras palavras, mesmo antes de descobrir a lei das áreas, Kepler tinha abandonado movimento circular uniforme como um princípio físico." Peter Barker & Bernard R. Goldstein, "Distance and Velocity in Kepler's Astronomy", Annals of Science, 51 (1994): 59–73, p. 60.
- Ir para cima↑ Koyré, The Astronomical Revolution, pp. 199–202
- Ir para cima↑ Caspar, Kepler, pp. 129–132
- Ir para cima↑ Caspar, Kepler, pp. 131–140; Koyré, The Astronomical Revolution, pp. 277–279
- Ir para cima↑ Caspar, Kepler, pp. 178–181
- Ir para cima↑ Caspar, Kepler, pp. 181–185. O título completo é Tertius Interveniens, das ist Warnung an etliche Theologos, Medicos vnd Philosophos, sonderlich D. Philippum Feselium, dass sie bey billicher Verwerffung der Sternguckerischen Aberglauben nict das Kindt mit dem Badt aussschütten vnd hiermit jhrer Profession vnwissendt zuwider handlen, traduzido por C. Doris Hellman como "Tertius Interveniens, que é um alerta para alguns teólogos, médicos e filósofos, especialmente D. Philip Feselius, que eles, em suas condenações baratas das superstições dos astrólogos, não joguem fora a criança com o banho e por esse meio, sem que saibam, ajam contrariamente às suas profissões."
- Ir para cima↑ Caspar, Kepler, pp. 192–197
- Ir para cima↑ Koestler, The Sleepwalkers p. 384
- Ir para cima↑ Caspar, Kepler, pp. 198–202
- Ir para cima↑ Lear, Kepler's Dream, pp. 1–78
- Ir para cima↑ Schneer, "Kepler's New Year's Gift of a Snowflake," pp. 531–545
- Ir para cima↑ Kepler, Johannes (1966) [1611]. Hardie, Colin, ed. De nive sexangula [The Six-sided Snowflake]. Oxford: Clarendon Press. OCLC 974730
- Ir para cima↑ Caspar, Kepler, pp. 202–204
- Ir para cima↑ Connor, Kepler's Witch, pp. 222–226; Caspar, Kepler, pp. 204–207
- Ir para cima↑ Caspar, Kepler, pp. 208–211
- Ir para cima↑ Caspar, Kepler, pp. 209–220, 227–240
- Ir para cima↑ Quotation from Connor, Kepler's Witch, p. 252, traduzido de uma carta de 23 de outubro de 1613 de Kepler a um homem nobre desconhecido.
- Ir para cima↑ Caspar, Kepler, pp. 220–223; Connor, Kepler's Witch, pp. 251–254.
- Ir para cima↑ Caspar, Kepler, pp. 239–240, 293–300
- ↑ Ir para:a b Gingerich, "Kepler, Johannes" from Dictionary of Scientific Biography, pp. 302–304
- Ir para cima↑ Wolf, A History of Science, Technology and Philosophy, pp. 140–141; Pannekoek, A History of Astronomy, p. 252
- Ir para cima↑ Caspar, Kepler, pp. 239, 300–301, 307–308
- Ir para cima↑ Caspar, Kepler, pp. 240–264; Connor, Kepler's Witch, capítulos I, XI–XIII; Lear, Kepler's Dream, pp. 21–39
- Ir para cima↑ Tradução de uma citação de Caspar (Kepler, pp. 265–266) traduzida do Harmonices Mundi
- Ir para cima↑ Caspar, Kepler, pp. 264–266, 290–293
- Ir para cima↑ Caspar, Kepler, pp. 266–290
- Ir para cima↑ Arthur I. Miller (24 de março de 2009). Deciphering the cosmic number: the strange friendship of Wolfgang Pauli and Carl Jung. [S.l.]: W. W. Norton & Company. p. 80. ISBN 9780393065329. Consultado em 7 de março de 2011
- Ir para cima↑ Westfall, Never at Rest, pp. 143, 152, 402–3; Toulmin and Goodfield, The Fabric of the Heavens, p. 248; De Gandt, 'Force and Geometry in Newton's Principia', chapter 2; Wolf, History of Science, Technology and Philosophy, p. 150; Westfall, The Construction of Modern Science, capítulos 7 e 8
- Ir para cima↑ Koyré, The Astronomical Revolution, p 502
- Ir para cima↑ Caspar, Kepler, pp. 308–328
- Ir para cima↑ Caspar, Kepler, pp. 332–351, 355–361
- Ir para cima↑ Koestler, The Sleepwalkers, p. 427.
- Ir para cima↑ Para um estudo detalhado acerca da recepção à astronomia de Kepler veja-se Wilbur Applebaum, "Keplerian Astronomy after Kepler: Researches and Problems," History of Science, 34(1996): 451–504.
- Ir para cima↑ Koyré, The Astronomical Revolution, pp.362–364
- Ir para cima↑ North, History of Astronomy and Cosmology, pp. 355–360
- Ir para cima↑ Albert van Helden, "The Importance of the Transit of Mercury of 1631,"Journal for the History of Astronomy, 7 (1976): 1–10.
- Ir para cima↑ HM Nautical Almanac Office (10 de junho de 2004). «1631 Transit of Venus». Consultado em 28 de agosto de 2006. Arquivado do original em 1 de outubro de 2006
- Ir para cima↑ Allan Chapman, "Jeremiah Horrocks, the transit of Venus, and the 'New Astronomy' in early 17th-century England," Quarterly Journal of the Royal Astronomical Society, 31 (1990): 333–357.
- Ir para cima↑ North, History of Astronomy and Cosmology, pp. 348–349
- Ir para cima↑ Wilbur Applebaum and Robert Hatch, "Boulliau, Mercator, and Horrock's Venus in sole visa: Three Unpublished Letters," Journal for the History of Astronomy, 14(1983): 166–179
- Ir para cima↑ Kuhn, The Copernican Revolution, pp. 238, 246–252
- Ir para cima↑ Jardine, "Koyré’s Kepler/Kepler's Koyré," pp. 363–367
- Ir para cima↑ Gingerich, introduction to Caspar's Kepler, pp. 3–4
- Ir para cima↑ Jardine, "Koyré’s Kepler/Kepler's Koyré," pp.367–372; Shapin, The Scientific Revolution, pp. 1–2
- Ir para cima↑ Stephen Toulmin, Review of The Sleepwalkers in The Journal of Philosophy, Vol. 59, no. 18 (1962), pp. 500–503
- Ir para cima↑ Pauli, "The Influence of Archetypical Ideas"
- Ir para cima↑ William Donahue, "A Novelist's Kepler," Journal for the History of Astronomy, Vol. 13 (1982), pp. 135–136; "Dancing the grave dance: Science, art and religion in John Banville's Kepler," English Studies, Vol. 86, no. 5 (October 2005), pp. 424–438
- Ir para cima↑ Marcelo Gleiser, "Kepler in the Dock", review of Gilder and Gilder's Heavenly Intrigue, Journal for the History of Astronomy, Vol. 35, pt. 4 (2004), pp. 487–489
- Ir para cima↑ Citação de Carl Sagan, Cosmos: A Personal Voyage, episódio III: "The Harmony of the Worlds". Kepler was hardly the first to combine physics and astronomy; however, according to the traditional (though disputed) interpretation of the Scientific Revolution, he would be the first astrophysicist in the era of modern science.
- Ir para cima↑ «Eggenberg Palace coin». Austrian Mint. Consultado em 9 de setembro de 2009
- Ir para cima↑ Ng, Jansen (3 de julho de 2009). «Kepler Mission Sets Out to Find Planets Using CCD Cameras». DailyTech. Consultado em 3 de julho de 2009
- A biografia mais completa de Kepler é a Kepler de Max Caspar. Embora existas muitas biografias mais recentes, a maioria delas baseia-se no trabalho de Caspar e contém pouquíssima pesquisa original; muitas das informações citadas por Caspar podem também ser encontradas em livros de Arthur Koestler, Kitty Ferguson, e James A. Connor. The Eye of Heaven de Owen Gingerich baseia-se na obra de Caspar para colocar Kepler no contexto intelectual mais amplo da astronomia moderna inicial. Muitos estudos posteriores concentraram-se em elementos específicos da sua vida e obra. A matemática de Kepler, visões cosmológicas, filosóficas e históricas têm sido extensivamente analisadas em livros e artigos, embora seu trabalho astrológico —e sua relação com sua astronomia— permaneça pouco estudado.
Bibliografia
- Andersen, Hanne; Peter Barker; and Xiang Chen. The Cognitive Structure of Scientific Revolutions, chapter 6: "The Copernican Revolution." New York: Cambridge University Press, 2006. ISBN 0-521-85575-6
- Armitage, Angus. John Kepler, Faber, 1966.
- Banville, John. Kepler, Martin, Secker and Warburg, London, 1981 (fictionalised biography)
- Barker, Peter and Bernard R. Goldstein: "Theological Foundations of Kepler's Astronomy". Osiris, Volume 16. Science in Theistic Contexts. University of Chicago Press, 2001, pp. 88–113
- Caspar, Max. Kepler; transl. and ed. by C. Doris Hellman; with a new introduction and references by Owen Gingerich; bibliographic citations by Owen Gingerich and Alain Segonds. New York: Dover, 1993. ISBN 0-486-67605-6
- Connor, James A. Kepler's Witch: An Astronomer's Discovery of Cosmic Order Amid Religious War, Political Intrigue, and the Heresy Trial of His Mother. HarperSanFrancisco, 2004. ISBN 0-06-052255-0
- De Gandt, Francois. Force and Geometry in Newton's Principia, Translated by Curtis Wilson, Princeton University Press 1995. ISBN 0-691-03367-6
- Dreyer, J. L. E. A History of Astronomy from Thales to Kepler. Dover Publications Inc, 1967. ISBN 0-486-60079-3
- Ferguson, Kitty. The nobleman and his housedog: Tycho Brahe and Johannes Kepler: the strange partnership that revolutionized science. London: Review, 2002. ISBN 0-7472-7022-8 – published in the US as: Tycho & Kepler: the unlikely partnership that forever changed our understanding of the heavens. New York: Walker, 2002. ISBN 0-8027-1390-4
- Field, J. V.. Kepler's geometrical cosmology. Chicago University Press, 1988. ISBN 0-226-24823-2
- Gilder, Joshua and Anne-Lee Gilder: Heavenly Intrigue: Johannes Kepler, Tycho Brahe, and the Murder Behind One of History's Greatest Scientific Discoveries, Doubleday (May 18, 2004). ISBN 0-385-50844-1 Reviews bookpage.com, crisismagazine.com
- Gingerich, Owen. The Eye of Heaven: Ptolemy, Copernicus, Kepler. American Institute of Physics, 1993. ISBN 0-88318-863-5 (Masters of modern physics; v. 7)
- Gingerich, Owen: "Kepler, Johannes" in Dictionary of Scientific Biography, Volume VII. Charles Coulston Gillispie, editor. New York: Charles Scribner's Sons, 1973
- Jardine, Nick: "Koyré’s Kepler/Kepler's Koyré," History of Science, Vol. 38 (2000), pp. 363–376
- Kepler, Johannes. Johannes Kepler New Astronomy trans. W. Donahue, forward by O. Gingerich, Cambridge University Press 1993. ISBN 0-521-30131-9
- Kepler, Johannes and Christian Frisch. Joannis Kepleri Astronomi Opera Omnia (John Kepler, Astronomer; Complete Works), 8 vols.(1858–1871). vol. 1, 1858, vol. 2, 1859, vol. 3,1860, vol. 6, 1866, vol. 7, 1868, Francofurti a.M. et Erlangae, Heyder & Zimmer, – Google Books
- Kepler, Johannes, et al. Great Books of the Western World. Volume 16: Ptolemy, Copernicus, Kepler, Chicago: Encyclopædia Britannica, Inc., 1952. (contains English translations by of Kepler's Epitome, Books IV & V and Harmonices Book 5)
- Koestler, Arthur. The Sleepwalkers: A History of Man's Changing Vision of the Universe. (1959). ISBN 0-14-019246-8
- Koyré, Alexandre: Galilean Studies Harvester Press 1977. ISBN 0-85527-354-2
- Koyré, Alexandre: The Astronomical Revolution: Copernicus-Kepler-Borelli Ithaca, NY: Cornell University Press, 1973. ISBN 0-8014-0504-1; Methuen, 1973. ISBN 0-416-76980-2; Hermann, 1973. ISBN 2-7056-5648-0
- Kuhn, Thomas S. The Copernican Revolution: Planetary Astronomy in the Development of Western Thought. Cambridge, MA: Harvard University Press, 1957. ISBN 0-674-17103-9
- Lindberg, David C.: "The Genesis of Kepler's Theory of Light: Light Metaphysics from Plotinus to Kepler." Osiris, N.S. 2. University of Chicago Press, 1986, pp. 5–42.
- Lear, John. Kepler's Dream. Berkeley: University of California Press, 1965
- North, John. The Fontana History of Astronomy and Cosmology, Fontana Press, 1994. ISBN 0-00-686177-6
- Pannekoek, Anton: A History of Astronomy, Dover Publications Inc 1989. ISBN 0-486-65994-1
- Pauli, Wolfgang. Wolfgang Pauli — Writings on physics and philosophy, translated by Robert Schlapp and edited by P. Enz and Karl von Meyenn (Springer Verlag, Berlin, 1994). See section 21, The influence of archetypical ideas on the scientific theories of Kepler, concerning Johannes Kepler and Robert Fludd (1574–1637). ISBN 3-540-56859-X
- Schneer, Cecil: "Kepler's New Year's Gift of a Snowflake." Isis, Volume 51, No. 4. University of Chicago Press, 1960, pp. 531–545.
- Shapin, Steven. The Scientific Revolution. Chicago: University of Chicago Press, 1996. ISBN 0-226-75020-5
- Stephenson, Bruce. Kepler's physical astronomy. New York: Springer, 1987. ISBN 0-387-96541-6 (Studies in the history of mathematics and physical sciences; 13); reprinted Princeton:Princeton Univ. Pr., 1994. ISBN 0-691-03652-7
- Stephenson, Bruce. The Music of the Heavens: Kepler's Harmonic Astronomy, Princeton University Press, 1994. ISBN 0-691-03439-7
- Toulmin, Stephen and June Goodfield. The Fabric of the Heavens: The Development of Astronomy and Dynamics. Pelican, 1963.
- Voelkel, James R. The Composition of Kepler's Astronomia nova, Princeton University Press, 2001. ISBN 0-691-00738-1
- Westfall, Richard S.. The Construction of Modern Science: Mechanism and Mechanics. John Wiley and Sons, 1971. ISBN 0-471-93531-X; reprinted Cambridge University Press, 1978. ISBN 0-521-29295-6
- Westfall, Richard S. Never at Rest: A Biography of Isaac Newton. Cambridge University Press, 1981. ISBN 0-521-23143-4
- Wolf, A. A History of Science, Technology and Philosophy in the 16th and 17th centuries. George Allen & Unwin, 1950.
- Barker, Peter and Bernard R. Goldstein: "Theological Foundations of Kepler's Astronomy". Osiris, Volume 16: Science in Theistic Contexts. University of Chicago Press, 2001, pp 88–113
- FONTAINE, Joëlle e SIMAAN, Arkan. A Imagem do Mundo dos Babilônios a Newton. São Paulo: Companhia das Letras, 2003.
- Kepler, Johannes, et al.: Great Books of the Western World. Volume 16: Ptolemy, Copernicus, Kepler , Chicago: Encyclopædia Britannica, Inc., 1952. (Contém traduções ao inglês de Epitome, de Kepler, Livros IV & V e Harmonices, Livro 5.)
- Kepler, Johannes: Johannes Kepler New Astronomy trans. W. Donahue, forward by O. Gingerich, Cambridge University Press 1993 ISBN 0-521-30131-9
- Kepler, Johannes, et al.: "Mysterium Cosmographicum"
- KOESTLER, Arthur, Os Sonâmbulos. São Paulo: Ibrasa, 1961).
- MOURÃO, Ronaldo Rogério de Freitas, Kepler: A descoberta das leis do movimento planetário. Rio de Janeiro: Odysseus, 2003.
- NEGUS, Kenneth G. The astrology of Kepler. Princeton, New Jersey: Eucopia Publications, 1987.
- Stephenson, Bruce: Kepler's physical astronomy. New York: Springer, 1987 ISBN 0-387-96541-6 (Studies in the history of mathematics and physical sciences; 13); reprinted Princeton:Princeton Univ. Pr., 1994 ISBN 0-691-03652-7
Wikipédia

















Nenhum comentário:
Postar um comentário